Effect of Roughness-Induced Dynamic Wheel Loading on Flexible Pavements
Master's Thesis
By: Johann J. Cárdenas
Adviser: Imad L. Al-Qadi
ICT is at the forefront of establishing means to quantify the impact of braking, accelerating, and cornering rolling conditions on the tire-pavement interaction. Research conducted in the last three decades at ICT has led to the development of state-of-the-art vehicle, tire and flexible pavement numerical models. The final document of this MS Thesis was published in May 2023 and can be publicly accessed here.
Please reference as follows if you wish to cite this work:
- Cardenas J., and Al-Qadi I. (2024) Impact of Road Roughness on Tire-Pavement Contact Stresses During Vehicle Maneuvering. ASCE Journal of Engineering Mechanics, 151(2). https://doi.org/10.1061/JENMDT.EMENG-7900
- Cardenas J., and Al-Qadi I. (2024) Impact of Dynamic Wheel Loading on Flexible Pavement Responses for Non-Free Rolling Conditions. Transportation Research Record, 2678(11) https://doi.org/10.1177/03611981241242378
Abstract
In this study, a decoupled vehicle–tire–pavement interaction model was used to establish a mechanistic framework to predict critical pavement responses. The response to roughness-induced dynamic wheel load (DWL) amplification and non-free rolling condition contact stresses were considered. State-of-the-art numerical models were used to account for pavement unevenness, vehicle dynamics, three-dimensional and non-uniform contact stresses, and the complex pavement material characteristics. The performed numerical simulations provided a means to analytically quantify the variation of vertical and in-plane contact stress distribution. That allowed the consideration of braking and acceleration scenarios. Hence, changes in strain field distribution and peak values for typical pavement structures under various axle configurations and axle loads were determined. Longitudinal and transverse tensile strains at the bottom of the asphalt concrete (AC) layer and shear strain in the AC layer, were found to be highly depended on the in-plane components of the contact stress distribution. Overlooking load amplification due to road roughness and impact of rolling conditions would results in unpredicting pavement distresses, such as bottom-up fatigue cracking, near-surface cracking, and rutting.
Objectives
- Estimating the impact of road roughness on dynamic load amplification for different axle weights and tire configurations, using a 21-DOF semi-trailer truck model.
- Quantifying the impact of roughness-induced DWL on the distribution of contact stresses during vehicle maneuvering conditions for different axle loads, speeds, and pavement conditions, using a three-dimensional (3D) hyperelastic finite element (FE) model of a Dual-Tire Assembly (DTA).
- Estimating the changes in flexible pavement bulk behavior and pavement responses regarding a static load under free rolling conditions when the calculated contact stresses are applied to relatively thin and thick flexible pavement structures.
Methodology
The reviewed framework to incorporate roughness-induced DWL into flexible pavement response prediction comprises four major steps, as illustrated in Figure 1:
- Step 01: Define a target IRI to generate an artificial multi-track road roughness profile for a given pavement condition using band-limited white noise (BLWN).
- Step 02: Utilize the multi-track road roughness profiles as input excitation to estimate the dynamic response of the mechanical 3D truck model and record the changes in axle load through time for a given traveling speed (dynamic load profile).
- Step 03: Conduct simulations using representative loads from the dynamic loading profile using a 3D FE tire model, to predict tire–pavement contact stresses.
- Step 04: Apply dynamic contact stresses to a 3D FE flexible pavement model using the continuous moving load approach to record pavement responses.
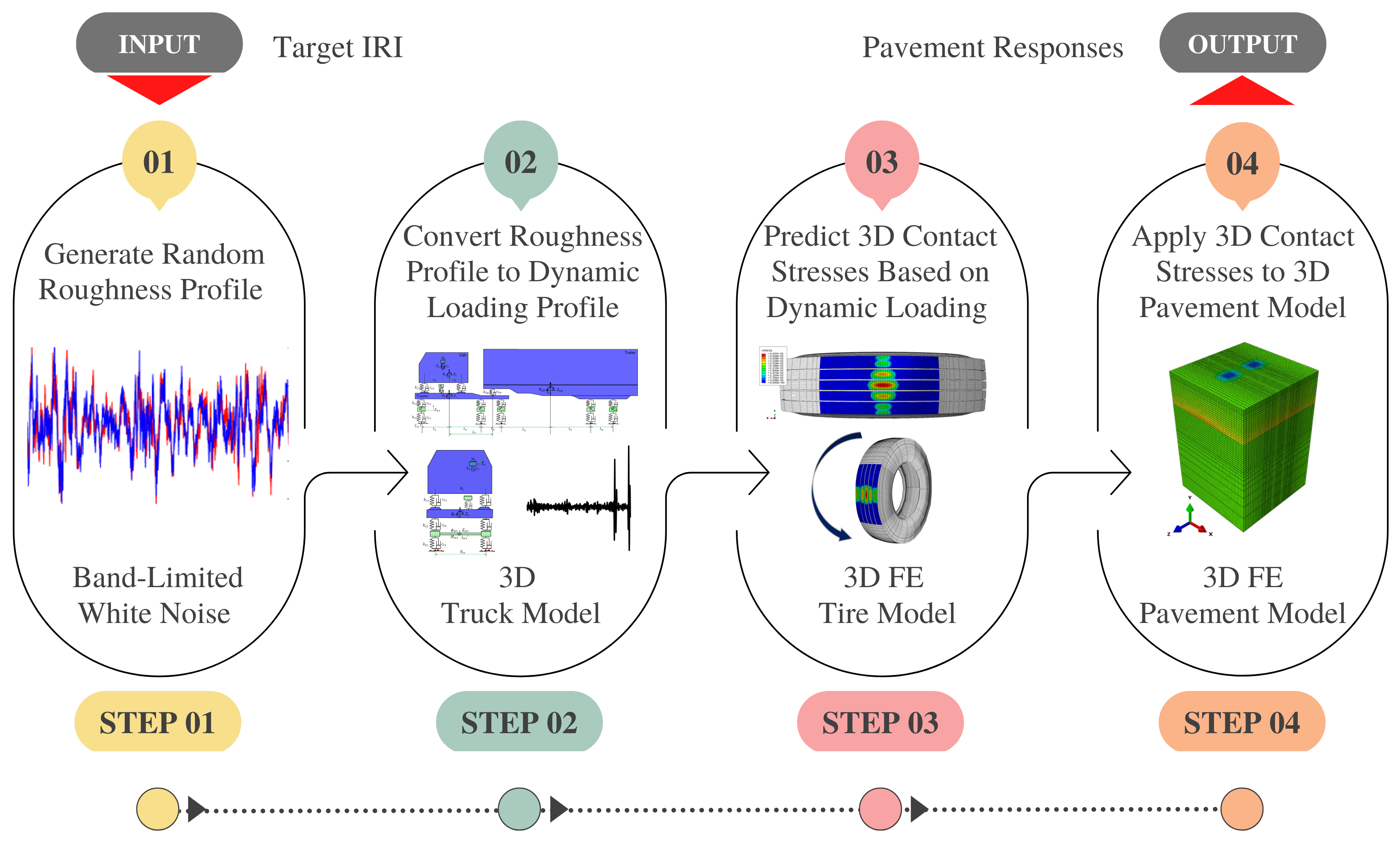
Fig 1. Impact of Dynamic Loading Framework
Three loading scenarios were defined by controlling the mechanical properties of the 21-DOF truck model such as the axle weight, trailer mass, tire stiffness and tire damping, as shown in Figure 2. The baseline scenario considered average values of steering-and drive-axle weights, using analyzed weigh-in-motion (WIM) data from across Illinois. Two possible distributions of extra weight derived from battery packs in electric trucks were assessed: i) battery weight is fully carried by the steering axle, and ii) battery weight is fully carried by the drive axle.
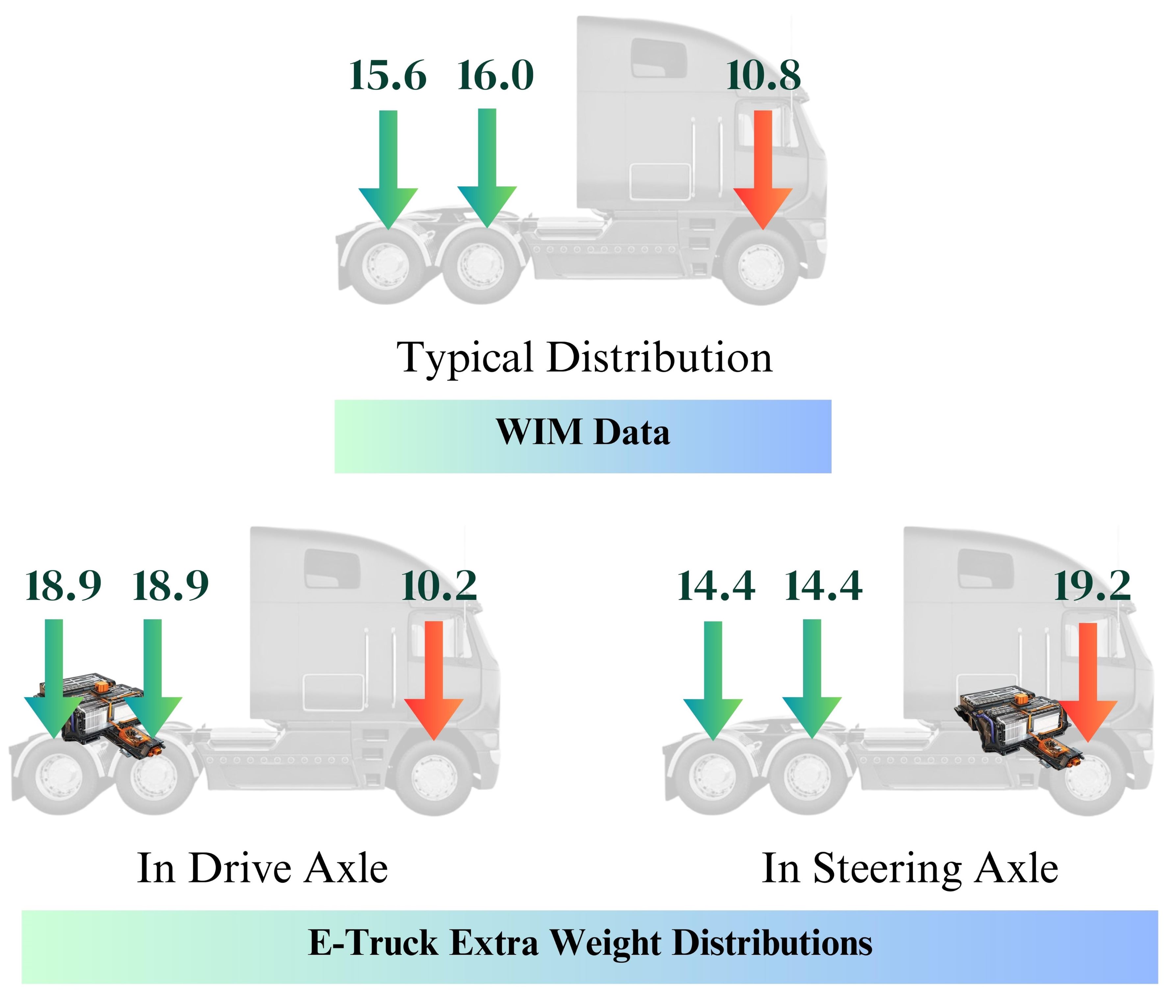
Fig 2. Axle Weight Distributions (in kips)
Results
- DWL amplification increased loads by up to 23%. The amplification is higher for stiffer tire types and wheel configurations.
- In-plane components of the contact stress distribution under vehicle maneuvering conditions differed considerably from that of the free-rolling condition. The horizontal component of the distribution increased from less than 1% of the vertical component to up to 23%.
- Full braking and full acceleration scenarios yielded similar absolute values of net horizontal force developed at the tire-pavement interface, but in opposite directions.
- At depths greater than 2-in from the surface, the critical responses yielded by the braking and acceleration cases were found to be equivalent.
- Under the most adverse conditions, the critical tensile strains at the bottom of the AC experienced an increase up to 125%, the shear strain increased up to 100% and the compressive strain escalated to 120% when compared to the reference case. Placing the battery pack at the steering axle was the most impactful scenario.
Two components of the strain field are highly associated with bottom-up fatigue cracking—the longitudinal tensile strain (𝝐11) and the transverse tensile strain (𝝐33) at the bottom of the AC layer. The shear strain (𝝐23) within the AC layer is linked to near-surface cracking and the vertical compressive strain (𝝐22) within each pavement layer is the primary factor in permanent deformation Figure 3 summarizes the increase in the critical strain values for the different axle configurations and axle loads:
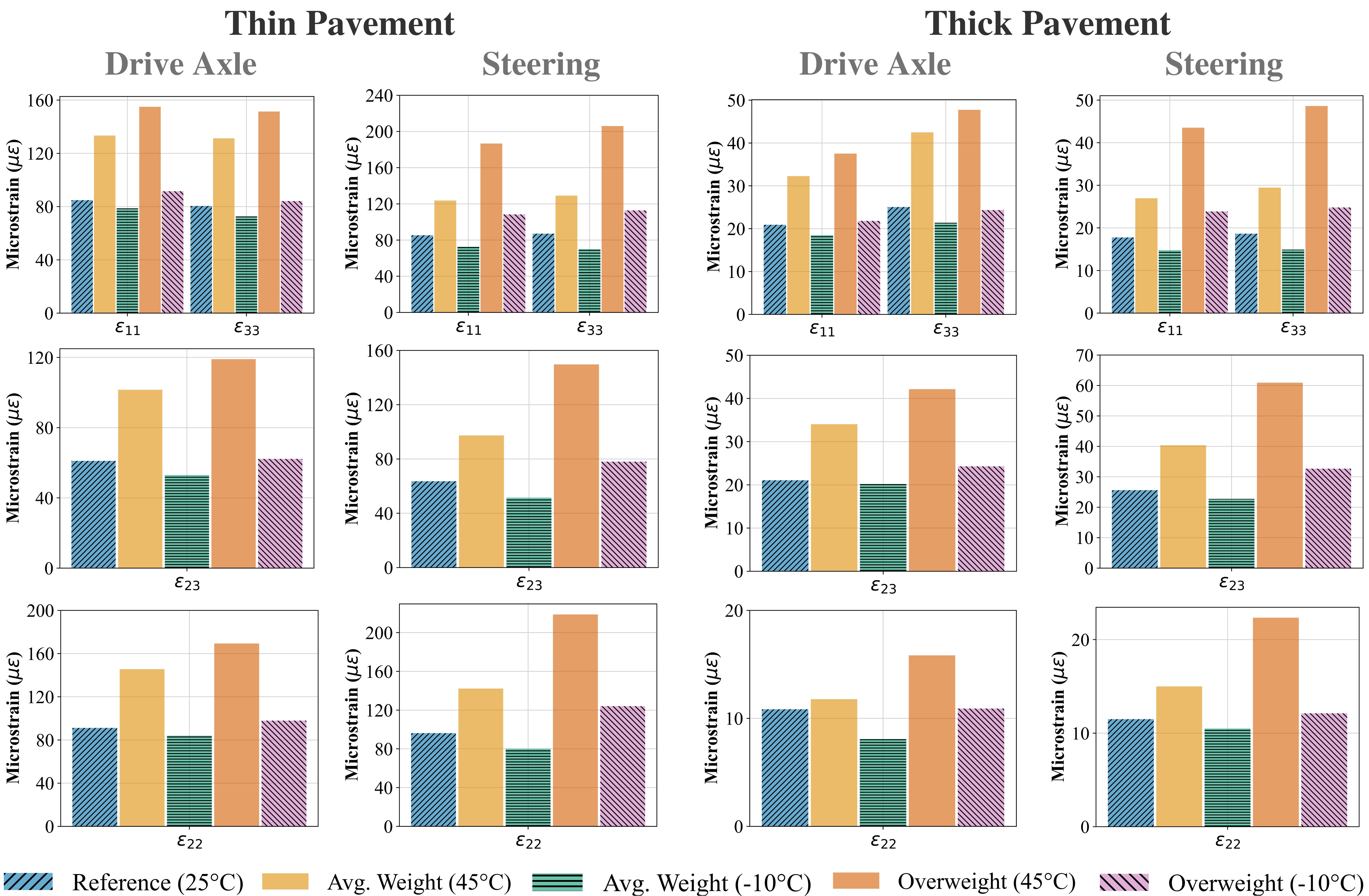
Fig 3. Main Strain Responses to Drive and Steering Axle within the AC Layer
Conclusions
- Free-rolling and static load conditions in pavement analysis would underpredict response to vehicular loading.
- Braking and accelerating contact stresses induced a different distribution and location for peak values at near-surface depths. These effects diminish with depth.
- In-plane contact stresses at the tire-pavement interface, during vehicle maneuvering, were greatly altered when considering roughness-induced dynamic loading and overweight axles. The effect on shear strain is set to accelerate near-surface pavement distresses.
- Critical pavement responses associated with bottom-up fatigue cracking, near-surface cracking and rutting were greatly altered due to the combined effect of road roughness, dynamic wheel load, overweight and temperature.
Last updated on January 4th, 2026